Introduction
In my most recent post, I summarised the various methods of Coronavirus modelling, ranging from phenomenological “curve-fitting” and statistical methods, to the SIR-type models which are developed from differential equations representing postulated incubation, infectivity, transmissibility, duration and immunity characteristics of the SARS-Cov-2 virus pandemic.
The phenomenological methods don’t delve into those postulated causations and transitions of people between Susceptible, Infected, Recovered and any other “compartments” of people for which a mechanistic model simulates the mechanisms of transfers (hence “mechanistic”).
Types of mechanistic SIR models
Some SIR-type mechanistic models can include temporary immunity (or no immunity) (SIRS) models, where the recovered person may return to the susceptible compartment after a period (or no period) of immunity.
SEIRS models allow for an Exposed compartment, for people who have been exposed to the virus, but whose infection is latent for a period, and so who are not infective yet. I discussed some options in my late March post on modelling work reported by the BBC.
My model, based on Alex de Visscher’s code, with my adaptations for the UK, has seven compartments – Uninfected, Infected, Sick, Seriously Sick, Better, Recovered and Deceased. There are many variations on this kind of model, which is described in my April 14th post on modelling progress.
Phenomenological curve-fitting
I have been focusing, in my review of modelling methods, on Prof. Michael Levitt’s curve-fitting approach, which seems to be a well-known example of such modelling, as reported in his recent paper. His small team have documented Covid-19 case and death statistics from many countries worldwide, and use a similar curve-fitting approach to fit current data, and then to forecast how the epidemics might progress, in all of those countries.
Because of the scale of such work, a time-efficient predictive curve-fitting algorithm is attractive, and they have found that a Gompertz function, with appropriately set parameters (three of them) can not only fit the published data in many cases, but also, via a mathematically derived display method for the curves, postulate a straight line predictor (on such “log” charts), facilitating rapid and accurate fitting and forecasting.
Such an approach makes no attempt to explain the way the virus works (not many models do) or to calibrate the rates of transition between the various compartments, which is attempted by the SIR-type models (although requiring tuning of the differential equation parameters for infection rates etc).
In response to the forecasts from these models, then, we see many questions being asked about why the infection rates, death rates and other measured statistics are as they are, differing quite widely from country to country.
There is so much unknown about how SARS-Cov-2 infects humans, and how Covid-19 infections progress; such data models inform the debate, and in calibrating the trajectory of the epidemic data, contribute to planning and policy as part of a family of forecasts.
The problem with data
I am going to make no attempt in this paper, or in my work generally, to model more widely than the UK.
What I have learned from my work so far, in the UK, is that published numbers for cases (particularly) and even, to some extent, for deaths can be unreliable (at worst), untimely and incomplete (often) and are also adjusted historically from time to time as duplication, omission and errors have come to light.
Every week, in the UK, there is a drop in numbers at weekends, recovered by increases in reported numbers on weekdays to catch up. In the UK, the four home countries (and even regions within them) collate and report data in different ways; as recently as July 17th, the Northern Ireland government have said that the won’t be reporting numbers at weekends.
Across the world, I would say it is impossible to compare statistics on a like-for-like basis with any confidence, especially given the differing cultural, demographic and geographical aspects; government policies, health service capabilities and capacities; and other characteristics across countries.
The extent of the (un)reliability in the reported numbers across nations worldwide (just like the variations in the four home UK countries, and in the regions), means that trying to forecast at a high level for all countries is very difficult. We also read of significant variations in the 50 states of the USA in such matters.
Hence my reluctance to be drawn into anything wider than monitoring and trying to predict UK numbers.
Curve fitting my UK model forecast
I thought it would be useful, at least for my understanding, to apply a phenomenological curve fitting approach to some of the UK reported data, and also to my SIR-style model forecast, based on that data.
I find the UK case numbers VERY inadequate for that purpose. There is a fair expectation that we are only seeing a minority fraction (as low as 8% in the early stages, in Italy for example) of the actual infections (cases) in the UK (and elsewhere).
The very definition of what comprises a case is somewhat variable; in the UK we talk about confirmed cases (by test), but the vast majority of people are never tested (owing to a lack of symptoms, and/or not being in hospital) although millions (9 million to date in the UK) of tests have either been done or requested (but not necessarily returned in all cases).
Reported numbers of tests might involve duplication since some people are (rightly) tested multiple times to monitor their condition. It must be almost impossible to make such interpretations consistently across large numbers of countries.
Even the officially reported UK deaths data is undeniably incomplete, since the “all settings” figures the UK Government reports (and at the outset even this had only been hospital deaths, with care homes added (and then retrospectively edited in later on) are not the “excess” deaths that the UK Office for National Statistics (ONS) also track, and that many commentators follow. For consistency I have continued to use the Government reported numbers, their having been updated historically on the same basis.
Rather than using case numbers, then, I will simply make the curve-fitting vs. mechanistic modelling comparison on both the UK reported deaths and the forecasted deaths in my model, which has tracked the reporting fairly well, with some recent adjustments (made necessary by the process of gradual and partial lockdown relaxation during June, I believe).
I had reduced the lockdown intervention effectiveness in my model by 0.5% at the end of June from 83.5% to 83%, because during the relaxations (both informal and formal) since the end of May, my modelled deaths had begun to lag the reported deaths during the month of June.
This isn’t surprising, and is an indicator to me, at least, that lockdown relaxation has somewhat reduced the rate of decline in cases, and subsequently deaths, in the UK.
My current forecast data
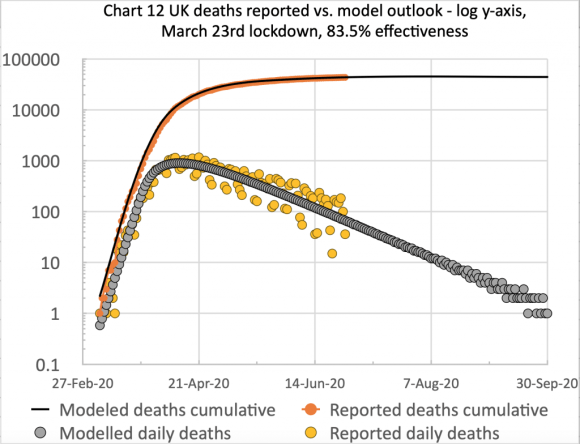
Firstly, I present my usual two charts summarising my model’s fit to reported UK data up to and including 16th July.

UK deaths, reported vs. model, 83%, cumulative, to 16th July 2020 
UK deaths, reported vs. model, 83%, cumulative and daily, to 16th July 2020
On the left we see the the typical form of the S-curve that epidemic cumulative data takes, and on the right, the scatter (the orange dots) in the reported daily data, mainly owing to regular incompleteness in weekend reporting, recovered during the following week, every week. I emphasise that the blue and grey curves are my model forecast, with appropriate parameters set for its differential equations (e.g. the 83% intervention effectiveness starting on March 23rd), and are not best fit analytical curves retro-applied to the data.
Next see my model forecast, further out to September 30th, by when forecast daily deaths have dropped to less than one per day, which I will also use to compare with the curve fitting approach. The cumulative deaths plateau, long term, is for 46,421 deaths in this forecast.

The curve-fitting Gompertz function
I have simplified the calculation of the Gompertz function, since I merely want to illustrate its relationship to my UK forecast – not to use it in anger as my main process, or to develop multiple variations for different countries. Firstly my own basic charts of reported and modelled deaths.

Cumulative, daily & 7-day avge reported UK deaths, 83%, 6th March – 16th July 
Cumulative, daily & 7-day avge model UK deaths, 83%, 6th March – 16th July
On the left we see the reported data, with the weekly variations I mentioned before (hence the 7-day average to make the trend clearer) and on the right, the modelled version, showing how close the fit is, up to 16th July.
On any given day, the 7-day average lags the barchart numbers when the numbers are growing, and exceeds the numbers when they are declining, as it is taking 7 numbers prior to and up to the reporting day, and averaging them. You can see this more clearly on the right for the smoother modelled numbers (where the averaging isn’t really necessary, of course).
It’s also worth mentioning that the Gompertz function fitting allows its analytical statistical function curve to fit the observed varying growth rate of this SARS-Cov-2 pandemic, with its asymmetry of a slower decline than the steeper ramp-up (sub-exponential though it is) as seen in the charts above.
I now add, to the reported data chart, a graphical version including a derivation of the Gompertz function (the green line) for which I show its straight line trend (the red line). The jagged appearance of the green Gompertz curve on the right is caused by the weekend variation in the reported data, mentioned before.

Reported & daily ratio of cumulative deaths, c(t)/c(t-1), and H(t) = Ln(c(t)/c(t-1)) 
Adding G(t), the negative natural log of H(t), in green, with its trend line in red
Those working in the field would use smoothed reported data to reduce this unnecessary clutter, but this adds a layer of complexity to the process, requiring its own justifications, whose detail (and different smoothing options) are out of proportion with this summary.
But for my model forecast, we will see a smoother rendition of the data going into this process. See Michael Levitt’s paper for a discussion of the smoothing options his team uses for data from the many countries the scope of his work includes.
Of course, there are no reported numbers beyond today’s date (16th July) so my next charts, again with the Gompertz equation lines added (in green), compare the fit of the Gompertz version of my model forecast up to July 16th (on the right) with the reported data version (on the left) from above – part of the comparison purpose of this exercise.

Adding the negative natural log of H(t) for reported data with its trend line in red 
Modelled daily ratio of cumulative deaths, c(t)/c(t-1), and H(t)=Ln(c(t)/c(t-1), and G(t)=-Ln(H(t)), to July 16th
The next charts, with the Gompertz equation lines added (in green), compare the fit of my model forecast only (i.e. not the reported data) up to July 16th on the left, with the forecast out to September 30th on the right.

Modelled daily ratio of cumulative deaths, c(t)/c(t-1) and H(t)=Ln(c(t)/c(t-1)), and G(t)=-Ln(H(t)), to 16th July 
Modelled daily ratio of cumulative deaths, c(t)/c(t-1), and H(t)=Ln(c(t)/c(t-1), and G(t)=-Ln(H(t)), to 30th Sept.
What is notable about the charts is the nearly straight line appearance of the Gompertz version of the data. The wiggles approaching late September on the right are caused by some gaps in the data, as some of the predicted model numbers for daily deaths are zero at that point; the ratios (c(t)/c(t-1)) and logarithmic calculation Ln(c(t)/c(t-1)) have some necessary gaps on some days (division by 0, and ln(0) being undefined).
Discussion
The Gompertz method potentially allows a straight line extrapolation of the reported data in this form, instead of developing SIR-style non-linear differential equations for every country. This means much less scientific and computer time to develop and process, so that Michael Levitt’s team can process many country datasets quickly, via the Gompertz functional representation of reported data, to create the required forecasts.
As stated before, this method doesn’t address the underlying mechanisms of the spread of the epidemic, but policy makers might sometimes simply need the “what” of the outlook, and not the “how” and “why”. The assessment of the infectivity and other disease characteristics, and the related estimation of their representation by coefficients in the differential equations for mechanistic models, might not be reliably and quickly done for this novel virus in so many different countries.
When policy makers need to know the potential impact of their interventions and actions, then mechanistic models can and do help with those dependencies, under appropriate assumptions.
As mentioned in my recent post on modelling methods, such mechanistic models might use mobility and demographic data to predict contact rates, and will, at some level of detail, model interventions such as social distancing, hygiene improvements and the use of masks, as well as self-isolation (or quarantine) for suspected cases, and for people in high risk groups (called shielding in the UK) such as the elderly or those with underlying health conditions.
Michael Levitt’s (and other) phenomenological methods don’t do this, since they are fitting chosen analytical functions to the (cleaned and smoothed) cases or deaths data, looking for patterns in the “output” data for the epidemic in a country, rather than for the causations for, and implications of the “input” data.
In Michael’s case, an important variable that is used is the ratio of successive days’ cases data, which means that the impact of national idiosyncrasies in data collection are minimised, since the same method is in use on successive days for the given country.
In reality, the parameters that define the shape (growth rate, inflection point and decline rate) of the specific Gompertz function used would also have to be estimated or calculated, with some advance idea of the plateau figure (what is called the “carrying capacity” of the related Generalised Logistics Functions (GLFs) of which the Gompertz functions comprise a subset).
I have taken some liberties here with the process, since my aim was simply to illustrate the technique using a forecast I already have.
Closing remarks
I have some corrective and clarification work to do on this methodology, but my intention has merely been to compare and contrast two methods of producing Covid-19 forecasts – phenomenological curve-fitting vs. SIR modelling.
These is much that the professionals in this field have yet to do. Many countries are struggling to move from blanket lockdown, through to a more targeted approach, using modelling to calibrate the changing effect of the various sub-measures in the lockdown package. I covered some of those differential effects of intervention options in my post on June 28th, including the consideration of any resulting “herd immunity” as a future impact of the relative efficacy of current intervention methods.
From a planning and policy perspective, Governments have to consider the collateral health impact of such interventions, which is why the excess deaths outlook is important, taking into account the indirect effect of both Covid-19 infections, and also the cumulative health impacts of the methods (such as quarantining and social distancing) used to contain the virus.
One of these negative impacts is on the take-up of diagnosis and treatment of other serious conditions which might well cause many further excess deaths next year, to which I referred in my modelling update post of July 6th, referencing a report by Health Data Research UK, quoting Data-Can.org.uk about the resulting cancer care issues in the UK.
Politicians also have to cope with the economic impact, which also feeds back into the nation’s health.
Hence the narrow numbers modelling I have been doing is only a partial perspective on a very much bigger set of problems.