Introduction
This is a very brief look at the model I have been working with for the last few months (thanks again to Prof Alex de Visscher for his original work on the model) to illustrate the sensitivities to lockdown easing settings as we move forward.
The UK Government has just announced some reversals of the current easings, and so before I model the new, additional interventions announced today, I want to illustrate quickly the behaviour of the model in response to changing the effectiveness of current interventions, to reflect the easings that have been made.
The history of UK Government changes, policies and announcements relating to Covid-19 be seen here at the Health Foundation website
Charts direct from the model
I can launch my Octave (MatLab) model direct from the Python code (developed by Dr. Tom Sutton) that interrogates the Worldometers UK reports. Similar information for the any country is available on related pages using the appropriate country code extension, eg for the US here.
The dates, cases and deaths data from Tom’s code are passed to the Octave model , which compares the reported data to the model data and plots charts accordingly.
I am showing just one chart 9, for brevity, in six successive versions as a slideshow, which makes it very clear how the successive relaxations of Government interventions (and public behaviour) are represented in the model, and affect the future forecast.
Model and reported UK deaths and cases from Feb 1st to Sep 12th with one easing of .3% 
Model and reported UK deaths and cases from Feb 1st to Sep 17th with 3 easings after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 17th with 4 easings after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 18th with 4 easings after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 20th with 5 easings after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 21st with 4 easings and 1 increase after the initial lockdown effectiveness of 84.3%,
By allowing the slideshow to run, we can see that the model is quite sensitive to the recent successive relaxations of epidemic interventions from Day 155 to Day 227 (July 4th to September 14th).
Charts from the model via spreadsheet analysis
I now show another view of the same data, this time plotted from a spreadsheet populated from the same Octave model, but with daily data plotted on the same charts, offering a little more insight.
Model and reported UK deaths and cases from Feb 1st to Sep 12th with just one easing of .03% after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 17th with 3 easings after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 17th with 4 easings after the initial lockdown effectiveness of 84.3%, as shown on the chart title 
Model and reported UK deaths and cases from Feb 1st to Sep 18th with 4 easings after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 20th with 5 easings after the initial lockdown effectiveness of 84.3% 
Model and reported UK deaths and cases from Feb 1st to Sep 21st with 5 easings and 1 increase after the initial lockdown effectiveness of 84.3%
Here, as well as the cumulative data, we see from the orange dots the scatter of daily reported deaths data (principally caused by lagged data reporting at weekends, with corresponding (upwards) correction in the following days) but also appearing more significant than it really is, because it is plotted at the lower part of the log scale, where the numbers are quite small for the amount of y-axis used to represent them (owing to the log scaling to fit both cumulative and daily reporting on the same chart).
As before, allowing the slideshow to play illustrates the marked effect on the forecast of the increases resulting from the easing of interventions, represented by the % changes to the intervention effectiveness.
This intervention effectiveness started at 84.3%, but on September 20th it was standing at only (84.3 -0.3 -4 -4 -4 -2)% = 70%, although in the last chart I have allowed a 2% increase in effectiveness to reflect some initial UK Government measures to get the virus under control again.
Discussion
The impact of easing of some interventions
As we can see from the model charts, with the UK lockdown relaxation (easing) status as at the last easing point in either presentation, September 14th, there is a quite significant upward tick in the death rate, which follows the earlier upward trend of cases in the UK, previously reported in my most recent post on September 2nd.
It is quite clear to me, in the charts and from the modelling behind them, that the UK’s lockdown, and subsequent series of easing points, has had a marked effect on the epidemic infection rate in the UK. Earlier modelling indicated that had the lockdown been a week or two earlier (I postulated and modelled a March 9th lockdown in particular, and discussed it in two posts on May 14th and June 11th), there would have been far fewer deaths from Covid-19. Prof. Neil Ferguson made this point in his answers to questions at the UK Parliamentary Science & Technology Select Committee on June 10th, as reported in my June 11th post.
Lately, we see that UK Government easing of some aspects of the March 23rd interventions is accompanied by an increase in case (infection) rates, which although more prevalent in the younger, working and socialising population, with a much lower risk of death, is feared to spill over into older parts of the population through families and friends; hence the further UK interventions to come on 24th September.
I am sure that these immediate strategies for controlling (“suppressing”) the epidemic are based on advice from the Scientific Advisory Group for Emergencies (SAGE), and through them by the Scientific Pandemic Influenza Group on Modelling (SPI-M) of which Neil Ferguson and his Imperial College group are part. Sir Patrick Vallance (Chief Scientific Adviser) and Prof. Chris Whitty (Chief Medical Officer), who sit on SAGE, made their own TV presentation direct to the public (with no politicians and no press questions) on 22nd September, outlining the scientific and medical opinions about where we are and where the epidemic is going. The full transcript is here.
Slides from the presentation:
7-day average cases and deaths per 100,000 for Spain and France 
Age-dependency in England of cases per 100,000, July to September 
Postulated outcome at the current growth rate of 7 day doubling time of cases per day by October 13th 
Less than 8% of people have antibiodies 
Geographical spread of Covid-19 in England 
Estimated new Covid-19 hospital admissions in England 
Progress on Vaccines
Returning to the modelling, I am happy to see that the Imperial College data sources, and their model codes are available on their website at https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/. The computer codes are written in the R language, which I have downloaded, as part of my own research, so I look forward to looking at them and reporting later on.
I always take time to mention the pivotal and influential March 16th Imperial College paper that preceded the first UK national lockdown on March 23rd, and the table from it that highlighted the many Non Pharmaceutical Interventions (NPIs) available to Government, and their relative effectiveness alone and in combinations.
I want to emphasise that in this paper, many optional strategies for interventions were considered, and critics of what they see as pessimistic forecasts of deaths in the paper have picked out the largest numbers, in the case of zero or minimal interventions, as if this were the only outcome considered.
The paper is far more nuanced than that, and the table below, while just one small extract, illustrates this. You can see the very wide range of possible outcomes depending on the mix of interventions applied, something I considered in my June 28th blog post.
Why was it, I had wondered, that in this chart (on the very last page of the paper, and referenced within it) the effectiveness of the three measures “CI_HQ_SD” in combination (home isolation of cases, household quarantine & large-scale general population social distancing) taken together (orange and yellow colour coding), was LESS than the effectiveness of either CI_HQ or CI_SD taken as a pair of interventions (mainly yellow and green colour coding)?
The answer to my query, from Imperial, was along the following lines, indicating the care to be taken when evaluating intervention options.
It’s a dynamical phenomenon. Remember mitigation is a set of temporary measures. The best you can do, if measures are temporary, is go from the “final size” of the unmitigated epidemic to a size which just gives herd immunity.
If interventions are “too” effective during the mitigation period (like CI_HQ_SD), they reduce transmission to the extent that herd immunity isn’t reached when they are lifted, leading to a substantial second wave. Put another way, there is an optimal effectiveness of mitigation interventions which is <100%.
That is CI_HQ_SDOL70 for the range of mitigation measures looked at in the report (mainly a green shaded column in the table above).
While, for suppression, one wants the most effective set of interventions possible.
All of this is predicated on people gaining immunity, of course. If immunity isn’t relatively long-lived (>1 year), mitigation becomes an (even) worse policy option.
This paper (and Harvard came to similar conclusions at that time) introduced (to me) the potential for a cyclical, multi-phase pandemic, which I discussed in my April 22nd report of the Cambridge Conversation I attended, and here is the relevant illustration from that meeting. This is all about the cyclicity of lockdown followed by easing, the population’s and pandemic’s responses, and repeats of that loop, just what we are seeing at the moment.
Key, however, to good modelling is good data, and this is changing all the time. The fine-grained nature of data about schools, travel patterns, work/home locations and the virus behaviour itself are quite beyond an individual to amass. It does require the resources of teams like those at Imperial College, the London School of Hygiene and Tropical Medicine, and in the USA, Harvard, Johns Hopkins and Washington Universities, to name just some prominent ones, whose groups embrace virological, epidemiological and mathematical expertise as well as (presumably) teams of research students to do much of the sifting of data.
Inferences for model types
In my September 2nd recent post, I drew some conclusions from my earlier investigation into mechanistic (bottom-up) and phenomenological/statistical (top-down, exemplified by curve-fitting) modelling techniques. I made it clear that the curve-fitting on its own, while indicative, offers no capability to model intervention methods yet to be made, nor changes in population and individual responses to those Government measures.
In discussing this with someone the other day, he usefully summarised such methods thus: “curve-fitting and least-squares fitting is OK for interpolation, but not for extrapolation”.
The ability of a model to reflect planned or postulated changes to intervention strategies and population responses is vital, as we can see from the many variations made in my model at the various lockdown easing points. Such mechanistic models – derived from realistic infection rates – also allow the case rates and resulting death rates to be assessed bottom-up as a check on reported figures, whereas curve-fitting models are designed only to fit the reported data (unless an overarching assumption is made about under-reporting).
The model shows up this facet of the UK reporting. As in many other countries, there is gross under-estimation of cases, partly because of the lack of a full test and trace system, and partly because testing is not universal. My model is forecasting much nearer to the realistic number of cases, as you will see below; conservatively, the reported numbers are only 10% of the likely infections, probably less.
My final model chart 10, where I have applied an 8.3 multiple to the reported cases to bring them into line with the model, illustrates this. You can just see from the chart, and of course from the daily reported numbers themselves at https://coronavirus.data.gov.uk, that the reported cases are already increasing sharply.
You can see from Chart 10 that the plateau for modelled cases is around 3 million. The under-reporting of cases (defining cases as those who have ever had Covid-19) was, in effect, confirmed by the major antibody testing programme, led by Imperial College London, involving over 100,000 people, finding that just under 6% of England’s population – an estimated 3.4 million people – had antibodies to Covid-19, and were therefore likely previously to have had the virus, prior to the end of June.
In this way, mechanistic models can highlight such deficiencies in reporting, as well as modelling the direct effects of intervention measures.
Age-dependency of risk
I have reported before on the startling age dependency of the risk of dying from Covid-19 once contracting it, most recently in my blog post on September 2nd where this chart presenting the changing age dependency of cases appeared, amongst others.
I mention this because the recent period of increasing cases in the UK, but with apparently a lower rate of deaths (although the deaths lag cases by a couple of weeks), has been attributed partly to the lower death risk of the younger (working and socialising) community whose infections are driving the figures. This has been even more noticeable as students have been returning to University.
The following chart from the BBC sourced from PHE data identifies that the caseload in the under-20s comprises predominantly teenagers rather than children of primary school age.
This has persuaded some to suggest, rather than the postulated restrictions on everyone, that older and more vulnerable people might shield themselves (in effect on a segregated basis) while younger people are more free to mingle. Even some of the older community are suggesting this. To me, that is “turkeys voting for Christmas” (you read it here first, even before the first Christmas jingles on TV ads!)
Not all older or more vulnerable people can, or want to segregate to that extent, and hitherto politicians have tended not to want to discriminate the current interventions in that way.
Scientists, of course, have looked at this, and I add the following by Adam Kucharski (of the modelling team at the London School of Hygiene and Tropical Medicine, and whose opinions I respect as well thought-out)) who presents the following chart in a recent tweet, from a paper authored by himself and others from several Universities about social mixing matrices, those Universities including Cambridge, Harvard and London.
Adam presents this chart, saying “For context, here’s data on pre-COVID social contacts between different age groups in UK outside home/work/school (from: https://medrxiv.org/content/10.1101/2020.02.16.20023754v2…). Dashed box shows over 65s reporting contacts with under 65s.
Adam further narrates this chart in a linked series of tweets on Twitter thus:
“I’m seeing more and more suggestions that groups at low risk of COVID-19 should go back to normal while high risk groups are protected. What would the logical implications of this be?
“First, let’s pick an example definition of risk. If we use infection fatality risk alone for simplicity (which of course isn’t only measure of severity), there is a clear age pattern, which rises above ~0.1% around age 50 and above ~1% around age 70 (https://medrxiv.org/content/10.1101/2020.08.24.20180851v1…)
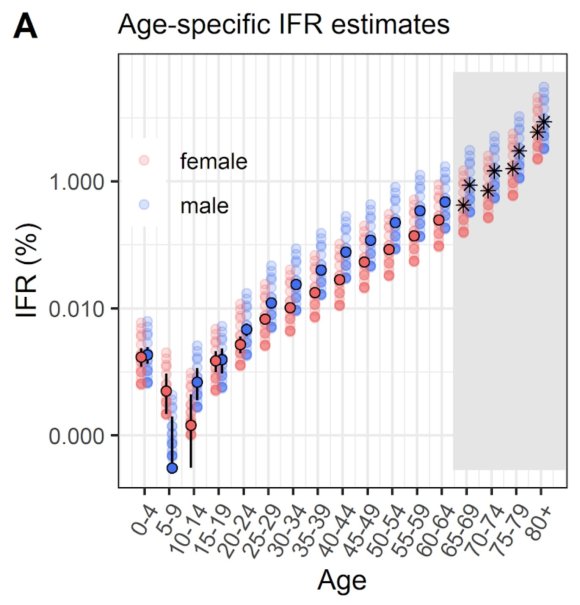
“Suppose hypothetically we define the over 65 age group as ‘high risk’. That’s about 18% of the UK population, and doesn’t include others with health conditions that put them at more at risk of severe COVID.
“The question, therefore, would be how to prevent any large outbreak among ‘low risk’ groups from spreading into ‘high risk’ ones without shutting these risk groups out of society for several months or more (if that were even feasible).
“There have been attempts to have ‘shielding’ of risk groups (either explicitly or implicitly) in many countries. But large epidemics have still tended to result in infection in these groups, because not all transmission routes were prevented.
“So in this hypothetical example, how to prevent contacts in the box from spreading infection into the over 65s? Removing interactions in that box would be removing a large part of people’s lives, but could the contacts be made less risky?
“One option would be to use rapid testing to make sure that these contacts are not infectious, e.g. testing attendees ahead of events/venues/gatherings. But remember, 18% of population are over 65, so that’s a lot of (low risk) contacts who would need to be tested regularly.
“Then there’s the question of what happens if contacts are positive… Would they need to self-isolate? People might well do anyway if they knew they’re infected, which could reduce wider transmission…
“Depending on what % of population is defined as at high risk, and how many contacts are tested regularly and isolate, could well get a situation where measures reduce transmission in the low risk groups too, leading to a low reproduction number.
“If this were to happen, it may become equivalent to a light-touch suppression approach via mass testing: https://twitter.com/AdamJKucharski/status/1303245754853658624?s=20…
“It wouldn’t be the first example of a situation where we start with two different approaches but end up with similar outcomes: https://twitter.com/AdamJKucharski/status/1292861098971070467?s=20…
“This thread obviously just picks a hypothetical example. But hopefully it shows it’s important to explore the logical implications of a particular scenario, because it won’t necessarily lead where we might initially assume.“
I have presented that thread pretty much verbatim (well, after all, I can’t deny a vested interest!) to indicate the complexity of the considerations.
His conclusion, in that last link on Twitter, was that “it illustrates that contact tracing and local lockdowns/quarantines aren’t a simple dichotomy – depending on how widely they are targeted, one can end up looking like the other, even if the initial approach is different.“
My own opinion is that it isn’t obviously feasible to isolate age-related parts of the community that way – speaking for myself, my own household spans such age groups.
Concluding comments
I support the temporary lockdown, learning the lessons from it and the moves to adjust it (downwards and upwards as judged necessary from sensible forecasts), drawing a balance between the nation’s health and the economic impacts, and I have no time for anything that smacks of anti-vaxxer or conspiracy theories, and anything that might encourage such crackpot ideas.
I’m afraid to say that some of the forecasts published on Twitter, and elsewhere, even by some well-qualified scientists who should know better (and presumably who have their own reasons for doing it – ambition, fame, politics…) do tend to encourage those with such opinions, and I’m very glad to see them called out. References available on application.
Added to the politicising, and subsequent refuting of simple precautions such as face-coverings and social distancing, one of the most dangerous tendencies (in the USA at least, but possibly on the increase here in the UK) is from those who say they won’t take a vaccine when available.
The current UK intervention measures are to be enhanced from tomorrow, September 23rd, following announcements today, as I write this post, and I will update the post to reflect a forecasting analysis including those announced changes.
