Month: June 2020

Introduction

A couple of interesting articles on the Coronavirus pandemic came to my attention this week; a recent one in National Geographic on June 26th, highlighting a startling comparison, between the USA’s cases history, and recent spike in case numbers, with the equivalent European data, referring to an older National Geographic article, from March, by Cathleen O’Grady, referencing a specific chart based on work from the Imperial College Covid-19 Response team.

I noticed, and was interested in that reference following a recent interaction I had with that team, regarding their influential March 16th paper. It prompted more thought about “herd immunity” from Covid-19 in the UK.

Meanwhile, my own forecasting model is still tracking published data quite well, although over the last couple of weeks I think the published rate of deaths is slightly above other forecasts as well as my own.

The USA

The recent National Geographic article from June 26th, by Nsikan Akpan, is a review of the current situation in the USA with regard to the recent increased number of new confirmed Coronavirus cases. A remarkable chart at the start of that article immediately took my attention:

The thrust of the article concerned recommendations on public attitudes, activities and behaviour in order to reduce the transmission of the virus. Even cases per 100,000 people, the case rate, is worse and growing in the USA.

A link between this dire situation and my discussion below about herd immunity is provided by a reported statement in The Times by Dr Anthony Fauci, Director of the National Institute of Allergy and Infectious Diseases, and one of the lead members of the Trump Administration’s White House Coronavirus Task Force, addressing the Covid-19 pandemic in the United States.

If the take-up of the vaccine were 70%, and it were 70% effective, this would result in roughly 50% herd immunity (0.7 x 0.7 = 0.49).

If the innate characteristics of the the SARS-CoV-2 virus don’t change (with regard to infectivity and duration), and there is no other human-to-human infection resistance to the infection not yet understood that might limit its transmission (there has been some debate about this latter point, but this blog author is not a virologist) then 50% is unlikely to be a sufficient level of population immunity.

My remarks later about the relative safety of vaccination (eg MMR) compared with the relevant diseases themselves (Rubella, Mumps and Measles in that case) might not be supported by the anti-Vaxxers in the US (one of whose leading lights is the disgraced British doctor, Andrew Wakefield).

This is just one more complication the USA will have in dealing with the Coronavirus crisis. It is one, at least, that in the UK we won’t face to anything like the same degree when the time comes.

The UK, and implications of the Imperial College modelling

That article is an interesting read, but my point here isn’t really about the USA (worrying though that is), but about a reference the article makes to some work in the UK, at Imperial College, regarding the effectiveness of various interventions that have been or might be made, in different combinations, work reported in the National Geographic back on March 20th, a pivotal time in the UK’s battle against the virus, and in the UK’s decision making process.

This chart reminded me of some queries I had made about the much-referenced paper by Neil Ferguson and his team at Imperial College, published on March 16th, that seemed (with others, such as the London School of Hygiene and Infectious Diseases) to have persuaded the UK Government towards a new approach in dealing with the pandemic, in mid to late March.

The thrust of this National Geographic article, by Cathleen O’Grady, was that we will need “herd immunity” at some stage, even if the Imperial College paper of March 16th (and other SAGE Committee advice, including from the Scientific Pandemic Influenza Group on Modelling (SPI-M)) had persuaded the Government to enforce several social distancing measures, and by March 23rd, a combination of measures known as UK “lockdown”, apparently abandoning the herd immunity approach.

The UK Government said that herd immunity had never been a strategy, even though it had been mentioned several times, in the Government daily public/press briefings, by Sir Patrick Vallance (UK Chief Scientific Adviser (CSA)) and Prof Chris Whitty (UK Chief Medical Officer (CMO)), the co-chairs of SAGE.

The particular part of the 16th March Imperial College paper I had queried with them a couple of weeks ago was this table, usefully colour coded (by them) to allow the relative effectiveness of the potential intervention measures in different combinations to be assessed visually.

Why was it, I wondered, that in this chart (on the very last page of the paper, and referenced within it) the effectiveness of the three measures “CI_HQ_SD” in combination (home isolation of cases, household quarantine & large-scale general population social distancing) taken together (orange and yellow colour coding), was LESS than the effectiveness of either CI_HQ or CI_SD taken as a pair of interventions (mainly yellow and green colour coding)?

The explanation for this was along the following lines.

It’s a dynamical phenomenon. Remember mitigation is a set of temporary measures. The best you can do, if measures are temporary, is go from the “final size” of the unmitigated epidemic to a size which just gives herd immunity.

If interventions are “too” effective during the mitigation period (like CI_HQ_SD), they reduce transmission to the extent that herd immunity isn’t reached when they are lifted, leading to a substantial second wave. Put another way, there is an optimal effectiveness of mitigation interventions which is <100%.

That is CI_HQ_SDOL70 for the range of mitigation measures looked at in the report (mainly a green shaded column in the table above).

While, for suppression, one wants the most effective set of interventions possible.

All of this is predicated on people gaining immunity, of course. If immunity isn’t relatively long-lived (>1 year), mitigation becomes an (even) worse policy option.

Herd Immunity

The impact of very effective lockdown on immunity in subsequent phases of lockdown relaxation was something I hadn’t included in my own (single phase) modelling. My model can only (at the moment) deal with one lockdown event, with a single-figure, averaged intervention effectiveness percentage starting at that point. Prior data is used to fit the model. It has served well so far, until the point (we have now reached) at which lockdown relaxations need to be modelled.

But in my outlook, potentially, to modelling lockdown relaxation, and the potential for a second (or multiple) wave(s), I had still been thinking only of higher % intervention effectiveness being better, without taking into account that negative feedback to the herd immunity characteristic, in any subsequent more relaxed phase, other than through the effect of the changing comparative compartment sizes in the SIR-style model differential equations.

I covered the 3-compartment SIR model in my blog post on April 8th, which links to my more technical derivation here, and more complex models (such as the Alex de Visscher 7-compartment model I use in modified form, and that I described on April 14th) that are based on this mathematical model methodology.

In that respect, the ability for the epidemic to reproduce, at a given time “t” depends on the relative sizes of the infected (I) vs. the susceptible (S, uninfected) compartments. If the R (recovered) compartment members don’t return to the S compartment (which would require a SIRS model, reflecting waning immunity, and transitions from R back to the S compartment) then the ability of the virus to find new victims is reducing as more people are infected. I discussed some of these variations in my post here on March 31st.

My method might have been to reduce the % intervention effectiveness from time to time (reflecting the partial relaxation of some lockdown measures, as Governments are now doing) and reimpose it to a higher % effectiveness if and when the R_t (the calculated R value at some time t into the epidemic) began to get out of control. For example, I might relax lockdown effectiveness from 90% to 70% when R_t reached R_t<0.7, and increase again to 90% when R_t reached R_t>1.2.

This was partly owing to the way the model is structured, and partly to the lack of disaggregated data I would have available to me for populating anything more sophisticated. Even then, the mathematics (differential equations) of  the cyclical modelling was going to be a challenge.

In the Imperial College paper, which does model the potential for cyclical peaks (see below), the “trigger” that is used to switch on and off the various intervention measures doesn’t relate to R_t, but to the required ICU bed occupancy. As discussed above, the intervention effectiveness measures are a much more finely drawn range of options, with their overall effectiveness differing both individually and in different combinations. This is illustrated in the paper (a slide presented in the April 17th Cambridge Conversation I reported in my blog article on Model Refinement on April 22nd):

What is being said here is that if we assume a temporary intervention, to be followed by a relaxation in (some of) the measures, the state in which the population is left with regard to immunity at the point of change is an important by-product to be taken into account in selecting the (combination of) the measures taken, meaning that the optimal intervention for the medium/long term future isn’t necessarily the highest % effectiveness measure or combined set of measures today.

The phrase “herd immunity” has been an ugly one, and the public and press winced somewhat (as I did) when it was first used by Sir Patrick Vallance; but it is the standard term for what is often the objective in population infection situations, and the National Geographic articles are a useful reminder of that, to me at least.

The arithmetic of herd immunity, the R number and the doubling period

I covered the relevance and derivation of the R₀ reproduction number in my post on SIR (Susceptible-Infected-Recovered) models on April 8th.

In the National Geographic paper by Cathleen O’Grady, a useful rule of thumb was implied, regarding the relationship between the herd immunity percentage required to control the growth of the epidemic, and the much-quoted R₀ reproduction number, interpreted sometimes as the number of people (in the susceptible population) one infected person infects on average at a given phase of the epidemic. When R_t reaches one or less, at a given time t into the epidemic, so that one person is infecting one or fewer people, on average, the epidemic is regarded as having stalled and to be under control.

Herd immunity and R₀

One example given was measles, which was stated to have a possible starting R₀ value of 18, in which case almost everyone in the population needs to act as a buffer between an infected person and a new potential host. Thus, if the starting R₀ number is to be reduced from 18 to R_t<=1, measles needs A VERY high rate of herd immunity – around 17/18ths, or ~95%, of people needing to be immune (non-susceptible). For measles, this is usually achieved by vaccine, not by dynamic disease growth. (Dr Fauci had mentioned over 95% success rate in the US previously for measles in the reported quotation above).

Similarly, if Covid-19, as seems to be the case, has a lower starting infection rate (R₀ number) than measles, nearer to between 2 and 3 (2.5, say (although this is probably less than it was in the UK during March; 3-4 might be nearer, given the epidemic case doubling times we were seeing at the beginning*), then the National Geographic article says that herd immunity should be achieved when around 60 percent of the population becomes immune to Covid-19. The required herd immunity H% is given by H% = (1 – (1/2.5))*100% ~= 60%.

Whatever the real Covid-19 innate infectivity, or reproduction number R₀ (but assuming R₀>1 so that we are in an epidemic situation), the required herd immunity H% is given by:

H%=(1-(1/R₀))*100%  (1)

(*I had noted that 80% was referenced by Prof. Chris Whitty (CMO) as loose talk, in an early UK daily briefing, when herd immunity was first mentioned, going on to mention 60% as more reasonable (my words). 80% herd immunity would correspond to R₀=5 in the formula above.)

R₀ and the Doubling time

As a reminder, I covered the topic of the cases doubling time T_D here; and showed how it is related to R₀ by the formula;

R₀=d(log_e2)/T_D  (2)

where d is the disease duration in days.

Thus, as I said in that paper, for a doubling period T_D of 3 days, say, and a disease duration d of 2 weeks, we would have R₀=14×0.7/3=3.266.

If the doubling period were 4 days, then we would have R₀=14×0.7/4=2.45.

As late as April 2nd, Matt Hancock (UK secretary of State for Health) was saying that the doubling period was between 3 and 4 days (although either 3 or 4 days each leads to quite different outcomes in an exponential growth situation) as I reported in my article on 3rd April. The Johns Hopkins comparative charts around that time were showing the UK doubling period for cases as a little under 3 days (see my March 24th article on this topic, where the following chart is shown.)

In my blog post of 31st March, I reported a BBC article on the epidemic, where the doubling period for cases was shown as 3 days, but for deaths it was between 2 and 3 days ) (a Johns Hopkins University chart).

Doubling time and Herd Immunity

Doubling time, T_D(t) and the reproduction number, R_t can be measured at any time t during the epidemic, and their measured values will depend on any interventions in place at the time, including various versions of social distancing. Once any social distancing reduces or stops, then these measured values are likely to change – T_D downwards and R_t upwards – as the virus finds it relatively easier to find victims.

Assuming no pharmacological interventions (e.g. vaccination) at such time t, the growth of the epidemic at that point will depend on its underlying R₀ and duration d (innate characteristics of the virus, if it hasn’t mutated**) and the prevailing immunity in the population – herd immunity. 

(**Mutation of the virus would be a concern. See this recent paper (not peer reviewed)

The doubling period T_D(t) might, therefore, have become higher after a phase of interventions, and correspondingly R_t < R₀, leading to some lockdown relaxation; but with any such interventions reduced or removed, the subsequent disease growth rate will depend on the interactions between the disease’s innate infectivity, its duration in any infected person, and how many uninfected people it can find – i.e. those without the herd immunity at that time.

These factors will determine the doubling time as this next phase develops, and bearing these dynamics in mind, it is interesting to see how all three of these factors – T_D(t), R_t and H(t) – might be related (remembering the time dependence – we might be at time t, and not necessarily at the outset of the epidemic, time zero).

Eliminating R from the two equations (1) and (2) above, we can find: 

H=1-T_D/d(log_e2) (3)

So for doubling period T_D=3 days, and disease duration d=14 days, H=0.7; i.e. the required herd immunity H% is 70% for control of the epidemic. (In this case, incidentally, remember from equation (2) that R₀=14×0.7/3=3.266.)

(Presumably this might be why Dr Fauci would settle for a 70-75% effective vaccine (the H% number), but that would assume 100% take-up, or, if less than 100%, additional immunity acquired by people who have recovered from the infection. But that acquired immunity, if it exists (I’m guessing it probably would) is of unknown duration. So many unknowns!)

For this example with 14 day infection period d, and exploring the reverse implications by requiring R_t to tend to 1 (so postulating in this way (somewhat mathematically pathologically) that the epidemic has stalled at time t) and expressing equation (2) as:

T_D (t)= d(log_e2)/R_t (4)

then we see that T_D(t)= 14*log_e(2) ~= 10 days, at this time t, for R_t~=1.

Thus a sufficiently long doubling period, with the necessary minimum doubling period depending on the disease duration d (14 days in this case), will be equivalent to the R_t value being low enough for the growth of the epidemic to be controlled – i.e. R_t <=1 – so that one person infects one or less people on average.

Confirming this, equation (3) tells us, for the parameters in this (somewhat mathematically pathological) example, that with T_D(t)=10 and d=14,

H(t) = 1 – (10/14*log_e(2)) ~= 1-1 ~= 0, at this time t.

In this situation, the herd immunity H(t) (at this time t) required is notionally zero, as we are not in epidemic conditions (R_t~=1). This is not to say that the epidemic cannot restart – it simply means that if these conditions are maintained, with R_t reducing to 1, and the doubling period being correspondingly long enough, possibly achieved through social distancing (temporarily), across whole or part of the population (which might be hard to sustain) then we are controlling the epidemic.

It is when the interventions are reduced, or removed altogether that the sufficiency of % herd immunity in the population will be tested, as we saw from the Imperial College answer to my question earlier. As they say in their paper:

“Once interventions are relaxed (in the example in Figure 3, from September onwards), infections begin to rise, resulting in a predicted peak epidemic later in the year. The more successful a strategy is at temporary suppression, the larger the later epidemic is predicted to be in the absence of vaccination, due to lesser build-up of herd immunity.“

Herd immunity summary

Usually herd immunity is achieved through vaccination (eg the MMR vaccination for Rubella, Mumps and Measles). It involves less risk than the symptoms and possible side-effects of the disease itself (for some diseases at least, if not for chicken-pox, for which I can recall parents hosting chick-pox parties to get it over and done with!)

The issue, of course, with Covid-19, is that no-one knows yet if such a vaccine can be developed, if it would be safe for humans, if it would work at scale, for how long it might confer immunity, and what the take-up would be.

Until a vaccine is developed, and until the duration of any CoVid-19 immunity (of recovered patients) is known, this route remains unavailable.

Hence, as the National Geographic article says, there is continued focus on social distancing, as an effective part of even a somewhat relaxed lockdown, to control transmission of the virus.

Is there an uptick in the UK?

All of the above context serves as a (lengthy) introduction to why I am monitoring the published figures at the moment, as the UK has been (informally as well as formally) relaxing some aspects of it lockdown, imposed on March 23rd, but with gradual changes since about the end of May, both in the public’s response and in some of the Government interventions.

My own forecasting model (based on the Alex de Visscher MatLab code, and my variations, implemented in the free Octave version of the MatLab code-base) is still tracking published data quite well, although over the last couple of weeks I think the published rate of deaths is slightly above other forecasts, as well as my own.

Worldometers forecast

The Worldometers forecast is showing higher forecast deaths in the UK than when I reported before – 47924 now vs. 43,962 when I last posted on this topic on June 11th:

My forecasts

The equivalent forecast from my own model still stands at 44,367 for September 30th, as can be seen from the charts below; but because we are still near the weekend, when the UK reported numbers are always lower, owing to data collection and reporting issues, I shall wait a day or two before updating my model to fit.

But having been watching this carefully for a few weeks, I do think that some unconscious public relaxation of social distancing in the fairer UK weather (in parks, on demonstrations and at beaches, as reported in the press since at least early June) might have something to do with a) case numbers, and b) subsequent numbers of deaths not falling at the expected rate. Here are two of my own charts that illustrate the situation.

In the first chart, we see the reported and modelled deaths to Sunday 28th June; this chart shows clearly that since the end of May, the reported deaths begin to exceed the model prediction, which had been quite accurate (even slightly pessimistic) up to that time.

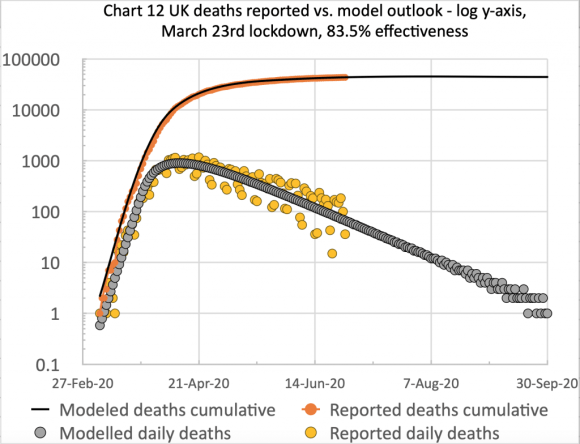
I will update this forecast in a day or two, once this last weekend’s variations in UK reporting are corrected.