Foreward
I am delighted that Roger Penrose, whose lectures I attended back in the late 60s, has become a Nobel laureate. It has come quite late (in his 80s), bearing in mind how long ago Roger, and then Stephen Hawking, had been working in the field of General Relativity, and Black Hole singularities in particular. I guess that recent astronomical observations, and the LIGO detection of gravitational waves at last have inspired confidence in those in Sweden deciding these matters.
I had the privilege, back in the day, of not only attending Roger’s lectures in London, but also the seminars by Stephen Hawking at DAMTP (Department of Applied Maths and Theoretical Physics, now the Isaac Newton Institute) in Cambridge, as well as lectures by Fred Hoyle, Paul Dirac and Martin Rees, amongst other leading lights.
Coming so late for Roger, and not at all, unfortunately, for Stephen Hawking, there is no danger of any “Nobel effect” for them (the tendency of some Nobel laureates either to not achieve much after their “enNobelment”(!) or to apply themselves, with overconfidence, to topics outside their speciality, to little effect, other than in a negative way on their reputation).
The remarkable thing about Roger Penrose is the breadth of his output in many areas of Mathematics over a very long career; and not only that, but the great modesty with which he carries himself. His many books illustrate the breadth of those interests.
I am delighted! If only my work below were worth a tiny fraction of his!
Coronavirus status
Many countries, including the UK, are experiencing a resurgence of Covid-19 cases recently, although, thankfully, with a much lower death rate. This is most likely owing to the younger age range of those being infected, and the greater experience and techniques that medical services have in treating the symptoms. I covered the age dependency in my most recent post on September 22nd, since when there has been a much higher rate of cases, with the death rate also increasing.
Model response
I have run several iterations of my model in the meantime, since my last blog post, as the situation has developed. There has been a remarkable increase in Covid-19 in the USA, as well as in many other countries.
I have introduced several lockdown adjustment points into my UK model, firstly easing the restrictions somewhat, to reflect things such as the return to schools, and other relaxations Governments in the four home UK countries have introduced, followed by some increases in interventions to reflect recent actions such as the “rule of six” and other related measures in the UK.
I’ll just show two charts initially to reflect the current status of the model. I am sure there will be some further “hardening” of interventions (exemplified in a later chart), and so the model forecast outcomes will, I expect, reduce as I introduce these when they come. I have already shown, in my recent post on model sensitivities, that the forecast is VERY sensitive to changes to intervention effectiveness in the model .
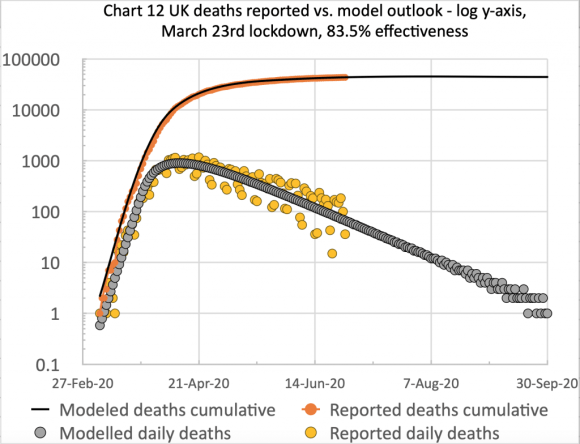
The first chart, from Excel, is of the type I have used before to show the cumulative and daily reported and modelled deaths on the same chart:

I have made no postulated interventions beyond October 6th in this model, but I fully expect some imminent interventions to bring down the forecast number of deaths.
The scatter in the orange dots (reported daily deaths) is caused by the regular under-reporting of deaths at weekends, followed by those deaths being added to the reports in the following couple of days of the week. Hence I show a 7-day trend line (the orange line) to smooth that effect.
The successive quantitative changes to the lockdown effectiveness are shown in the chart title, the initial UK lockdown having occurred on March 23rd.
The following chart, plotted straight from the Octave model code, shows the model versions of the lockdown and subsequent interventions in more detail, including dates. It also includes reported and modelled cases as well as deaths data, both cumulative and daily.

This is quite a busy chart. Again we see the clustering of reported data (this time for reported cases as well as reported deaths) owing to the reporting delays at weekends.
The key feature is the sharp rise in cases, and to a lesser extent, deaths, around the time of the lockdown easing in the summer. The outcomes at the right for April 2021 will be modified (reduced), I believe, by measures yet to be taken that have already been trailed by UK Government.
The forecasts from the model are to the right of the chart, at Day 451, April 26th 2021. The figures presented there are the residual statistics at that point. In the centre of the chart are the reported cumulative and daily figures as at October 8th. The lockdown easing dates and setting percentages are listed in the centre of the chart, in date order.
Data accuracy, and Worldometers
The charts are based on the latest daily updates, and also corrections made in the UK case data, owing to the errors caused at Public Health England (PHE) by the use of a legacy version of the Excel spreadsheet system by some of their staff. That older Excel version loses data, owing to a limit on the number of lines it can handle in a table (c. 64,000 (or, more likely, 216-1) instead of millions in current versions of Excel).
Thus (to increase reader confidence(!)) I haven’t run the Excel chart again for the charts that follow. I am indebted to Dr. Tom Sutton for his Worldometers interrogation script, which allows me to collect Worldometers data and run model changes quickly, with current data, and plot the results, using Python for the data interrogation, and Octave (the GNU free version of MatLab) to run the model and plot results, fed by the UK data from the Worldometers UK page.
Tom’s Python “corona-fetch” code allows me to extract any country’s data rapidly from Worldometers, in which I have some confidence. They updated the UK data, and cast it back to the correct days between September 25th and October 4th, following the UK Government’s initial October 2nd announcement of the errors in their reporting.
Worldometers did this before I was able to find the corrected historic data on the UK Government’s own Coronavirus reporting page – it might not yet even be there for those previous days; the missing data first appeared only as much inflated numbers for the days on that October 2nd-4th weekend.
Case under-reporting
As I highlighted in my September 22nd post, I believe that reported cases are under-reported in the UK by a factor of over 8 – i.e. less than 12.5% of cases are being picked up, in my view, owing to a lack of testing, and the high proportion of asymptomatic infections, resulting in fewer requested tests.
The under-reporting of cases (defining cases as those who have ever had Covid-19) was, in effect, confirmed by the major antibody testing programme, led by Imperial College London, involving over 100,000 people, finding that just under 6% of England’s population – an estimated 3.4 million people – had antibodies to Covid-19, and were therefore likely previously to have had the virus, prior to the end of June.
The USA
For interest, I ran the model for the USA at the same time, as it is so easy to source the USA Worldometers data. Only one lockdown event is shown in my model charts for the US, as I don’t have detailed data for the US on Government actions and population and individual reactions, on which I have done more work for the UK – the USA not being my principal focus.
I would expect there should be some intervention easing settings in the summer period for the USA, judging by what we have seen of the growth in the USA’s numbers of cases and deaths during that period.
Those relaxations, both at state level and individually, have, in my view, frustrated many forecasts (some made somewhat rashly, and not couched with caveats), including the one by Michael Levitt made as recently as mid-July for August 25th (to which I referred in some detail in my September 2nd post) when both the quantum of the US numbers, and the upwards slope for deaths and cases were quite contrary to his expectation. We can see that reflected in my model’s unamended figures, following the 74% effective March 24th lockdown event, representing the first somewhat serious reaction to the epidemic in the USA.
This is the problem, in my view, with curve-fitting (phenomenological) forecasts used on their own, as compared with mechanistic models such as mine, whose code was originally developed by Prof. Alex de Visscher at Concordia University.
All that curve-fitting is does is to perform a least-squares fit of a 3 or 4 parameter Logistics curve of some kind (Sigmoid, Roberts or Gompertz curve) top-down, with no bottom-up way to reflect Government strategies and population/individual reactions. Curve-fitting can give a fast graphical interpolation of data, but isn’t so suitable for extrapolating a forecast of any worthwhile duration.
This chart below, without the benefit of the introduction of subsequent intervention measures, shows how a forecast can begin to undershoot reality, until the underlying context can be introduced. Lockdown easing events (both formal and informal since March 24th) need to be added to allow the model to show their potential consequences for increased cases and deaths, and thus for the model to be calibrated for projections beyond the present day, October 8th.

Effect of a UK “circuit-breaker” intervention
There is current discussion of a (2 week) “circuit-breaker” partial lockdown in the UK, coinciding with schools’ half-term, and the Government seems to be considering a tiered version of this, with the areas with higher caseloads making stricter interventions. There would be differences in the policy within the four home UK countries, but all of them have interventions in mind, for that half-term period, as cases are increasing in them all.
I have postulated, therefore, an exemplar increased intervention. I have applied a 10% increase in current intervention effectiveness on October 19th (although there are some differences in the half-term dates across the UK), followed by a partial relaxation after 2 weeks, -5%, reducing the circuit-breaker measure by half – so not back to the level we are at currently.
Here is the effect of that change on the model forecast.

As one might expect for an infection with a 7-14 day incubation period, although the effect on reducing new infections (daily cases) is fairly rapid, this is lagged somewhat by the effect on the death rate; but over the medium and longer term, this change, just as for the original lockdown, reduces the severity of the modelled outcome materially.
I don’t think any models have the capability yet to reflect very detailed interventions, local and regional as they are becoming, to deal with local outbreaks in a context where much of the country is less affected. What we have been seeing are what I have called “multiple superspreader” events, and potentially a new modelling methodology, reflecting Adam Kucharski’s “k-number” concept of over-dispersion would be needed. I covered this in more detail in my August 4th blog post.
Discussion
As I reported in my blog post on May 14th, if the original lockdown had been 2 weeks earlier than March 23rd (and this principle was supported in principle by scientists reporting to the Parliamentary Science and Technology Select Committee on June 10th, which I reported in my blog post on June 11th), there would have been far fewer deaths; the UK Government is likely to want to avoid any delay this time around.
October 19th might well be later than they would wish, and so earlier interventions, varying locally and/or regionally are likely.
While the forecast of a model is critically dependent not only on the model logic, and its virus infectivity parameters, the decisions to be taken about interventions, and their timing, critically impact the epidemic and the modelled outcomes.
A model like this offers a way to calibrate and test the effect of different changes. My model does that in a rather broad-brush way, using successive broad intervention effectiveness parameters at chosen times.
Imperial College analysis
Models used by Government advisers are more sophisticated, and as I reported last time, the Imperial College data sources, and their model codes are available on their website at https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/. Both Imperial College and Harvard University have published their outlook on cyclical behaviour of the pandemic; in the Imperial case, the triggering of interventions and any relaxations were modelled on varying ICU bed occupancy, but it could be also be done, I suppose, though R-number thresholds (upwards and downwards) at any stage. Here is the Imperial chart; the Harvard one was similar, projected into 2022.

The Imperial computer codes are written in the R language, which I have downloaded, as part of my own research, so I look forward to looking at them and reporting later on.
I know that their models allow very detailed analysis of options such as social distancing, home isolation and/or quarantining, schools/University closure and many other possible interventions, as can be seen from the following chart which I have shown before, from the pivotal and influential March 16th Imperial College paper that preceded the first UK national lockdown on March 23rd.
It is usefully colour-coded by the authors so that the more and less effective options can be more easily discerned.

An intriguing point is that in this chart (on the very last page of the paper, and referenced within it) the effectiveness of the three measures “CI_HQ_SD” in combination (home isolation of cases, household quarantine & large-scale general population social distancing) taken together (orange and yellow colour coding), was LESS than the effectiveness of either CI_HQ or CI_SD taken as a pair of interventions (mainly yellow and green colour coding)?
The answer to my query, from Imperial, was along the following lines, indicating the care to be taken when evaluating intervention options.
It’s a dynamical phenomenon. Remember mitigation is a set of temporary measures. The best you can do, if measures are temporary, is go from the “final size” of the unmitigated epidemic to a size which just gives herd immunity.
If interventions are “too” effective during the mitigation period (like CI_HQ_SD), they reduce transmission to the extent that herd immunity isn’t reached when they are lifted, leading to a substantial second wave. Put another way, there is an optimal effectiveness of mitigation interventions which is <100%.
That is CI_HQ_SDOL70 for the range of mitigation measures looked at in the report (mainly a green shaded column in the table above).
While, for suppression, one wants the most effective set of interventions possible.
All of this is predicated on people gaining immunity, of course. If immunity isn’t relatively long-lived (>1 year), mitigation becomes an (even) worse policy option.
This paper (and Harvard came to similar conclusions at that time, as we see in the additional chart below) introduced (to me) the potential for a cyclical, multi-phase pandemic, which I discussed in my April 22nd report of the Cambridge Conversation I attended, and here is the relevant illustration from that meeting.

In the absence of a pharmaceutical solution (e.g. a vaccine) this is all about the cyclicity of lockdown followed by easing; then the population’s and pandemic’s responses; and repeats of that loop, just what we are beginning to see at the moment.
Second opinion on the Imperial model code
Scientists at the School of Physics and Astronomy, University of Edinburgh have used the Imperial College CovidSim code to run the data and check outcomes, reported in the British Medical Journal (BMJ), in their paper Effect of school closures on mortality from coronavirus disease 2019: old and new predictions.
Their conclusions were broadly supportive of the veracity of the modelling tool, and commenting on their results, they say:
“The CovidSim model would have produced a good forecast of the subsequent data if initialised with a reproduction number of about 3.5 for covid-19. The model predicted that school closures and isolation of younger people would increase the total number of deaths, albeit postponed to a second and subsequent waves. The findings of this study suggest that prompt interventions were shown to be highly effective at reducing peak demand for intensive care unit (ICU) beds but also prolong the epidemic, in some cases resulting in more deaths long term. This happens because covid-19 related mortality is highly skewed towards older age groups. In the absence of an effective vaccination programme, none of the proposed mitigation strategies in the UK would reduce the predicted total number of deaths below 200 000.“
Their overall conclusion was:
“It was predicted in March 2020 that in response to covid-19 a broad lockdown, as opposed to a focus on shielding the most vulnerable members of society, would reduce immediate demand for ICU beds at the cost of more deaths long term. The optimal strategy for saving lives in a covid-19 epidemic is different from that anticipated for an influenza epidemic with a different mortality age profile.“
This is consistent with the table above, and with the explanation given to me by Imperial quoted above. The lockdown can be “too good” and optimisation for the medium/long term isn’t the same as short term optimisation.
I intend to run the Imperial code myself, but I am very glad to see this second opinion. There have been many responses to it, so I will devote a later blog post to it.
Concluding Comments
As we see, a great deal of multidisciplinary work is proceeding in many Universities and other organisations around the world. Virologists, epidemiologists, clinicians, mathematicians and many others are involved in working out solutions to the issues raised in all countries by the SARS-Cov-2 pandemic.
A vaccine must be top of the list for dealing with it, and until then, the best that we can do as members of the public is to recognise the key indicators for staying safe, some of them mentioned above in relation to the NPIs.
We have seen that in the spring and summer period it was possible to make progress with opening up the economy, but as the easing of interventions begins to coincide with autumn, the return to schools and Universities, and the increasing pressure to revive not just our economy, but also social interactions, cases have increased, and the test will continue to be how to control the spread of the virus while allowing some “normal” activities to return.
The studies I have mentioned, as well as my own work indicate clearly the complexity, and in some respects the counter-intuitive nature of managing the epidemic. There is much more to do.